

We can also see that the r-squared for the regression model is r 2 = 0.9602. This is the proportion of the variance in the response variable that can be explained by the explanatory variables. Happiness = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09Ĭonversely, an individual that works 30 hours perk week is predicted to have a happiness level of 92.99: We can use this equation to find the predicted happiness of an individual, given the number of hours they work per week.įor example, an individual that works 60 hours per week is predicted to have a happiness level of 22.09: so that all the data points will be clearly visible on the calculator screen. Happiness = -0.1012(hours) 2 + 6.7444(hours) – 18.2536 Quadratic Regression is a process by which the equation of a parabola of. Higher-order polynomials are possible (such as quadratic. The following output will automatically appear:įrom the results, we can see that the estimated regression equation is as follows: This includes the mean average and linear regression which are both types of polynomial regression. Scroll down to Calculate and press Enter. Press Stat and then scroll over to CALC. Then scroll down to 5: QuadReg and press Enter.įor Xlist and Ylist, make sure L1 and L2 are selected since these are the columns we used to input our data. Next, we will perform quadratic regression.
This upside down “U” shape in the scatterplot indicates that there is a quadratic relationship between hours worked and happiness, which means we should use quadratic regression to quantify this relationship. We can see that happiness tends to increase as number of hours worked increases from zero up to a certain point, but then begins to drop lower as the number of hours worked increases further. This will automatically produce the following scatterplot: Next, press zoom and then press 9:ZoomStat.
Make sure the plot is on and that L1 and L2 are selected for Xlist and Ylist, respectively: Next, press 2nd and then press y= to access the statplot menu. Enter the following values for the explanatory variable (hours worked) in column L1 and the values for the response variable (happiness) in column L2: Use the following steps to perform a quadratic regression on a TI-84 calculator.īefore we can use quadratic regression, we need to make sure that the relationship between the explanatory variable (hours) and response variable (happiness) is actually quadratic.įirst, we will input the data values for both the explanatory and the response variable. Press Stat and then press EDIT . We have the following data on the number of hours worked per week and the reported happiness level (on a scale of 0-100) for 11 different people: Suppose we are interested in understanding the relationship between number of hours worked and happiness. Example: Quadratic Regression on a TI-84 Calculator
#Quadratic regression calculator how to
This tutorial explains how to perform quadratic regression on a TI-84 Calculator. However, when two variables have a quadratic relationship, we can instead use quadratic regression to quantify their relationship. The maximum of this parabola is at x = 7.2871, which suggests that the optimal ticket price is around $7.28.When two variables have a linear relationship, we can often use simple linear regression to quantify their relationship.

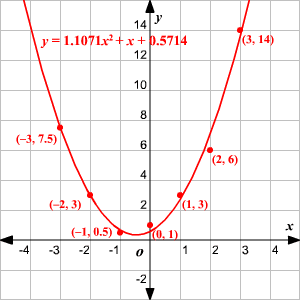
Using the quadratic regression calculator above, the best fit second-degree polynomial is The admin collects the following data in which X is the price of tickets and Y is the gross admissions revenues: By definition of r, this will have a correlation of 1.Ī museum administrator assumes that the gross daily revenue from admissions is a quadratic function of the ticket price. For instance, if you perform quadratic regression on three points, you will find the equation of the parabola that passed through the three points exactly. When the sample is small, the value of r may not indicate the true level of fit. If r is low, you should check your data to see whether a quadratic equation is the most appropriate model for the points.įor quadratic regression on a large number of points, the formula for r is When the coefficient is close to 1, it indicates good fit. The coefficient of correlation r measures how well the quadratic equation fits the data. If the 3-by-3 matrix on the left is invertible, then there is a unique set of values for a, b, and c that minimizes the function F(a, b, c). Where n is the number of data points (x i, y i).


 0 kommentar(er)
0 kommentar(er)
